MENU
HaukunProject 3rdGen. Ver.8.1 | はぅ君プロジェクト

型くりこ「Bezier Glyph/ベジェグリフ」について

プロジェクト
Processing 型くりこ(TypeOfCreativeCoding)

型くりこについてはこちらをご覧ください。

目次

「Bezier Glyph/ベジェグリフ」について

直線やベジェ曲線などを使って、架空の文字のような記号を描く技法です。

座標や位置などにある程度ルールを設け、そのルールの中でランダムさを入れた線を描くことで見た目が文字っぽくなります。作品のアクセントやワンポイントとして使いやすいので私もよく使用しています。フォントの著作権なども気にしなくてよいですしね。

Asemic writingという概念があるようでして、おそらくそこに属する技法になるのかと思います。

使い方

ルールを用意し、そのルールの中でrandom()やnoise()を利用して座標を決めて線を引きます。

今回は「円状に60度ごとの点があるとして、そこからランダムに二つの点を選んで線を引く」というルールにしてみます。

ちなみに縦長にすると、より文字っぽくなります。

円状に60度ごとに点があるとして、いずれかの点を2つ選んで直線を複数本描くと、その組み合わせが文字のように見える。
void setup(){
  size(720, 720, P2D);
  background(192);
  noFill();
  
  for(int x = 0; x < width; x+= 60){
    for(int i = 0; i < 4; i++){
      float r1 = int(random(6)) * PI / 3; // 60度上のいずれかの点を選ぶ
      float r2 = int(random(6)) * PI / 3;
      
      float px1 = cos(r1) * 30 + x;
      float py1 = sin(r1) * 60 + height /2;
      
      float px2 = cos(r2) * 30 + x;
      float py2 = sin(r2) * 60 + height /2;
            
      line(px1, py1, px2, py2);
    }
  }
}
function setup(){
  createCanvas(720, 720);
  background(192);
  noFill();
  
  for(var x = 0; x < width; x+= 60){
    for(var i = 0; i < 3; i++){
      var r1 = int(random(6)) * PI / 3; // 60度上のいずれかの点を選ぶ
      var r2 = int(random(6)) * PI / 3;
      
      var px1 = cos(r1) * 30 + x;
      var py1 = sin(r1) * 60 + height /2;
      
      var px2 = cos(r2) * 30 + x;
      var py2 = sin(r2) * 60 + height /2;
            
      line(px1, py1, px2, py2);
    }
  }
}
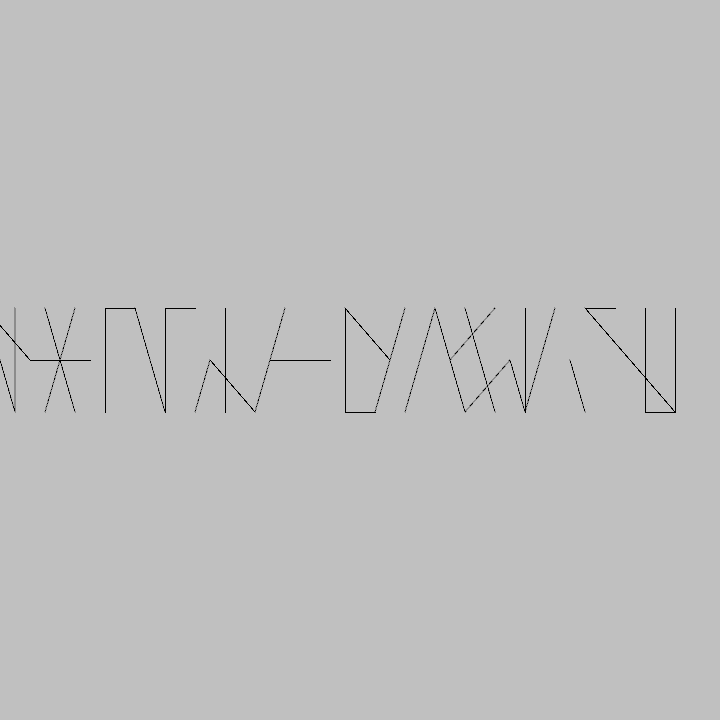
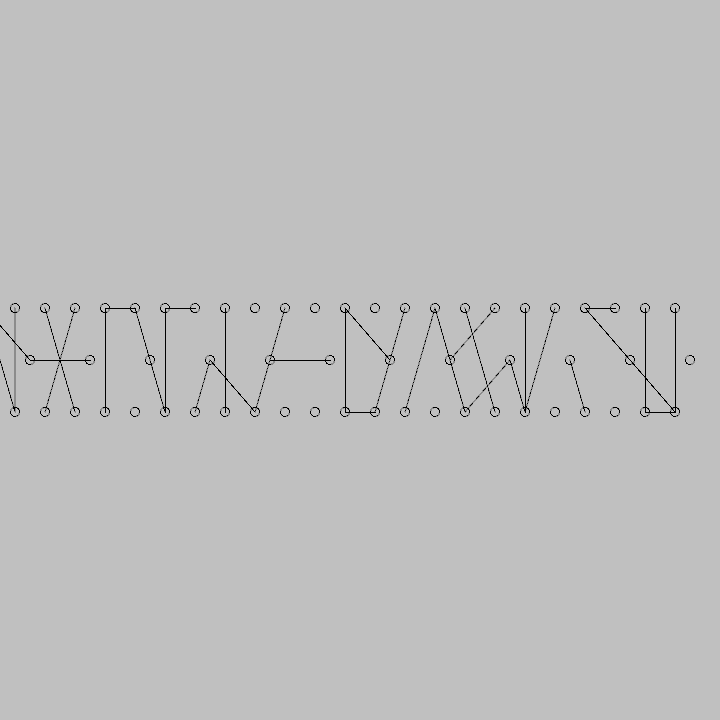
0度と180度の位置（円状の右と左）は隣の円状と重なる位置にしていて、その線の繋がりも文字っぽさを想起させる。
円状の60度ごとの位置に円を描いてみると、各直線がルール（いずれかの円から円へ線を引く）に沿って引かれていることがわかる。

追加説明

直線ではなく曲線を使用するとより手書きの文字っぽくなります。今回はベジェ曲線を使用してみます。

void setup(){
  size(720, 720, P2D);
  background(192);
  noFill();
  
  for(int x = 0; x < width; x+= 60){
    for(int i = 0; i < 3; i++){
      float r1 = int(random(6)) * PI / 3; // 60度上のいずれかの点を選ぶ
      float r2 = int(random(6)) * PI / 3;
      float rc1 = int(random(6)) * PI / 3;
      float rc2 = int(random(6)) * PI / 3;
      
      float px1 = cos(r1) * 30 + x;
      float py1 = sin(r1) * 60 + height / 2;
      
      float px2 = cos(r2) * 30 + x;
      float py2 = sin(r2) * 60 + height / 2;
      
      float cx1 = cos(rc1) * 30 + x;
      float cy1 = sin(rc1) * 60 + height / 2;
      
      float cx2 = cos(rc2) * 30 + x;
      float cy2 = sin(rc2) * 60 + height / 2;
      
      bezier(px1, py1, cx1, cy1, cx2, cy2, px2, py2);
    }
  }
}
function setup(){
  createCanvas(720, 720);
  background(192);
  noFill();
  
  for(var x = 0; x < width; x+= 60){
    for(var i = 0; i < 3; i++){
      var r1 = int(random(6)) * PI / 3; // 60度上のいずれかの点を選ぶ
      var r2 = int(random(6)) * PI / 3;
      var rc1 = int(random(6)) * PI / 3;
      var rc2 = int(random(6)) * PI / 3;
      
      var px1 = cos(r1) * 30 + x;
      var py1 = sin(r1) * 60 + height / 2;
      
      var px2 = cos(r2) * 30 + x;
      var py2 = sin(r2) * 60 + height / 2;
      
      var cx1 = cos(rc1) * 30 + x;
      var cy1 = sin(rc1) * 60 + height / 2;
      
      var cx2 = cos(rc2) * 30 + x;
      var cy2 = sin(rc2) * 60 + height / 2;
      
      bezier(px1, py1, cx1, cy1, cx2, cy2, px2, py2);
    }
  }
}
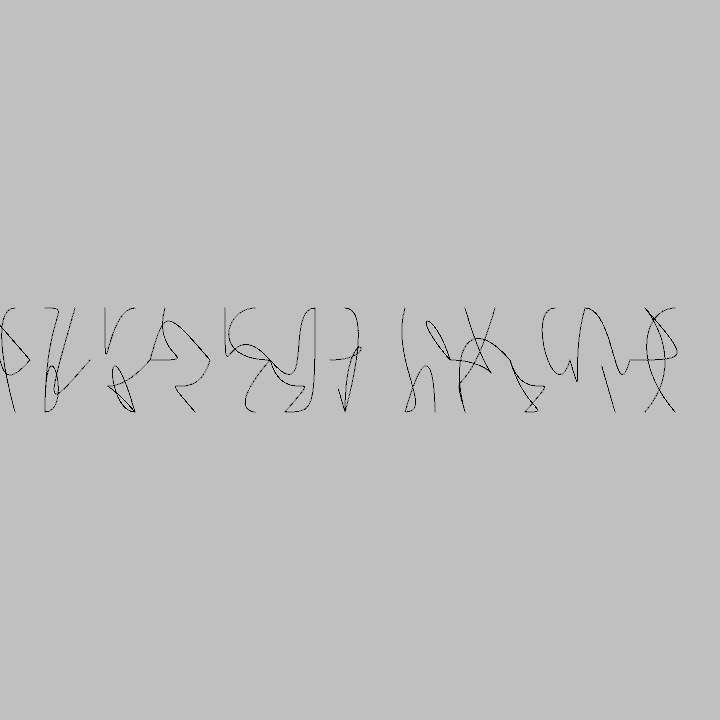
bezier()の第3～6引数のコントロールポイントによって複雑な曲線が描かれる。
円状の60度ごとの位置から別の位置へと線を引くというルールは変わらない。

応用編

文字の配置を工夫することで様々に応用が可能です。例えば下記の型くりこ「Archimedes’ Spiral/アルキメデスの螺旋」と組み合わせることができます。

あわせて読みたい
型くりこ「Archimedes’ spiral/アルキメデスの螺旋」について 螺旋状に図形を配置していく技法です。

型くりこ「Bezier Glyph/ベジェグリフ」を型くりこ「Archimedes’ Spiral/アルキメデスの螺旋」を使って配置してみた例。

void setup(){
  size(720, 720, P2D);
  background(192);
  noFill();
  
  for(float r = 0; r < TAU * 9; r += 0.1){
    for(int i = 0; i < 3; i++){
      float r1 = int(random(6)) * PI / 3; 
      float r2 = int(random(6)) * PI / 3;
      float rc1 = int(random(6)) * PI / 3;
      float rc2 = int(random(6)) * PI / 3;
      
      float px1 = cos(r1) * 10;
      float py1 = sin(r1) * 20;
      
      float px2 = cos(r2) * 10;
      float py2 = sin(r2) * 20;
      
      float cx1 = cos(rc1) * 10;
      float cy1 = sin(rc1) * 20;
      
      float cx2 = cos(rc2) * 10;
      float cy2 = sin(rc2) * 20;
      
      push();
      translate(cos(r) * r * 9 + width / 2, sin(r) * r * 9 + height /2);
      rotate(r + PI / 2); // 右側から開始するため90度回転する
      bezier(px1, py1, cx1, cy1, cx2, cy2, px2, py2);
      pop();
    }
  }
}
function setup(){
  createCanvas(720, 720);
  background(192);
  noFill();
  
  for(var r = 0; r < TAU * 9; r += 0.1){
    for(var i = 0; i < 3; i++){
      var r1 = int(random(6)) * PI / 3; 
      var r2 = int(random(6)) * PI / 3;
      var rc1 = int(random(6)) * PI / 3;
      var rc2 = int(random(6)) * PI / 3;
      
      var px1 = cos(r1) * 10;
      var py1 = sin(r1) * 20;
      
      var px2 = cos(r2) * 10;
      var py2 = sin(r2) * 20;
      
      var cx1 = cos(rc1) * 10;
      var cy1 = sin(rc1) * 20;
      
      var cx2 = cos(rc2) * 10;
      var cy2 = sin(rc2) * 20;
      
      push();
      translate(cos(r) * r * 9 + width / 2, sin(r) * r * 9 + height /2);
      rotate(r + PI / 2); // 右側から開始するため90度回転する
      bezier(px1, py1, cx1, cy1, cx2, cy2, px2, py2);
      pop();
    }
  }
}

その他作品

型くりこ「Bezier Glyph/ベジェグリフ」の考え方を使った作品をいくつか紹介いたします。

#つぶやきProcessing になってしまっているので、コードは圧縮されている箇所が多いですが、基本的な考え方は本記事に記載した内容と同等です。

プロジェクト
Processing 型くりこ(TypeOfCreativeCoding)
  • URLをコピーしました！

コメント

コメントする

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。

目次